< 암호학 > 페르마의 이론, 오일러의 이론
Fetmat's Theorem 페르마의 이론
Fetmat's Little Theorem으로도 알려져있다.
소수 p에 대하여, p와 서로소인 a에 대하여 다음 식이 성립한다.

단, 다음 두 조건을 잘 확인해야 한다.
1. p는 소수이다.
2. 1을 만족하고 a < p 이다.
= gcd(a,p) = 1, a는 p와 서로소와 같은 의미이다.
p가 소수라면, p보다 작은 약수는 1과 p뿐이기 때문이다.
이 이론은 암호학의 공유키 활용, 소수 검증에서 많이 사용한다.
증명은 하지 않고 활용에 초점을 둔다 ..
< 활용 예시 >
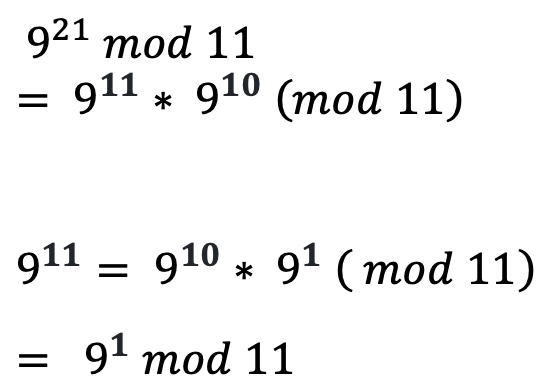
이와 같은 매우 큰 지수승 계산을 쉽게 만들 수 있습니다.
그 이유는

9와 11이 조건을 만족하여 페르마의 이론이 성립하기 때문입니다.
Euler Totient Function φ(n) 오일러 피 함수
- complete set of residues : 0부터 n-1
- reduced set of residues : 0부터 n-1까지 중 서로소들 집합
오일러 피 함수는 이 "reduced set of residues"의 개수를 반환하는 함수이다.
1. n이 소수인 경우
φ(n) = p-1
ex) φ(37) = 36
>>소수는 (스스로 제외) 전부 서로소기 때문에
2. n이 두 소수 p,q 의 곱인 경우
φ(pq) = φ(p) * φ(q) = (p-1)*(q-1)
ex) φ(21) = (3-1) * (7-1) = 12
>> 21 = 3*7이므로
Euler's Theorem 오일러의 이론
오일러 이론은 위의 페르마 이론을 일반화합니다.
1. n이 소수가 아니지만, a와 n이 서로소인 경우

이 수식의 조건은 다음과 같습니다.
는 n과 서로소, (gcd(a,n)=1 인 정수여야 합니다.
2. a와 n이 서로소가 아니지만, n이 서로 다른 두 소수의 곱인 경우
이 수식의 조건은 다음과 같습니다.

과 가 ϕ(n)을 기준으로 동일한 나머지를 가진다면,
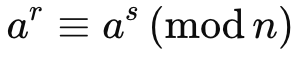
모든 정수 a에 대하여 위 식이 성립합니다.
< 예시 >
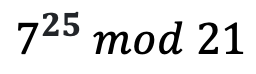
이 문제는 21이 소수가 아닌데다 25와 서로소가 아니기 때문에 첫번째 오일러의 이론을 사용할 수 없습니다.
따라서 두번쨰 수식에 적용이 가능한지 살펴보면,
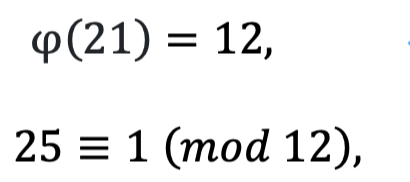
21의 오일러 피 함수값은 12입니다.
7의 25제곱을 쉽게 바꿔야 하므로, mod 12에 대하여 25와 합동인 수를 찾아보면, 1이라는 값이 있음을 알 수 있습니다.

이 수식에서 r는 25, s는 1, n은 21이 되어 성립하는 것을 알 수 있습니다.
따라서 모든 integer a에 대하여 다음 수식을 적용할 수 있으므로, 구해야하는 값에 따라 a를 7로 놓고 수식을 적용하면 다음과 같습니다.
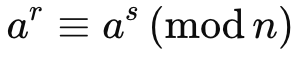

즉 mod 21에서 7의 25제곱은 7과 합동으로, 결과는 7입니다.
더불어 오일러 정리에 따라 다음식이 성립하므로,
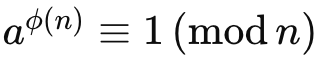
아래와 같은 식도 성립합니다.
